History of Indian Science
Ho Peng Yoke
Ho Peng Yoke 何丙郁, born 4 April 1926 in Kinta Valley, died 18 October, 2014 in Brisbane was a Malaya-born historian of Chinese science, whose work in Australia, the UK, and Hong Kong contributed greatly to its understanding in Anglophone academia. After a distinguished career at Griffith University, where he was Chairman (1973-78) and Foundation Professor of the School of Modern Asian Studies, he became the director of the Needham Research Institute from 1990-2001. He was a Fellow of the Australian Academy of the Humanities and an Academician of Academia Sinica.
History of Indian Science
(a lecture given during the 1970’s at the University of Queensland at the invitation of Professor D.P. Singhal)
The earliest Indian contribution to science lies in the field of medicine. According to Hindu tradition, in the time of the Buddha (6th century B.C.) there were two great universities in India, one in the East at KaSi (or Benares) and one in the west, at Taksasila (or Taxila on the Jhelam river). Atreya, the physician, taught in the latter, while Susruta, the surgeon, in the former. Modern scholars disagree among themselves regarding the exact periods when Atreya and Susruta flourished, and have placed their limits between 6th century B.C. and 5th century A.D. The work of Susruta is one of the greatest of its kind in Sanskrit literature, and is specially important from the surgical point of view. It describes a number of operations, including the removal of cataract and hernia, the Caesarian section, and so on. It even deals with plastic surgery, the use of the magnet as a surgical instrument and a great variety of other surgical instruments. It also concerns itself with anatomy, physiology, pathology, obstetrics, pediatrics and medicinal plants. The work of Atreya was represented by the Kashmirian physician Caraka (fl. c. 120/162 A.D.) who wrote a medical compendium called the Caraka samhita. An edition of Susuta’s treatise is also ascribed to Nagarjuna (2nd/3rd century A.D.), one of the creators of Mahayana Buddhism.
The earliest Hindu works on astronomy are the so-called siddhantas, which are large treatises of mainly a theoretical nature. Later on there were also works of more practical nature, called the karanas and there appeared also commentaries and astronomical tables. There were 5 siddhantas, namely the Surya-Siddhanta, the Paitamaha-Siddhanta, the Vasishtha-Siddhanta, the Paulisa-Siddhanta and the Romaka-Siddhanta. Of these only the first, the Surya-Siddhanta is extant in its original form. We do not know exactly when the siddhantas were written, but it is highly probable that they were not all written at the same period. All of them show some Greek influence to a greater or less degree. This is least conspicuous in the Paitamaha and most conspicuous in the Romaka. The Greek influence appears to be of a post-Ptolemaic nature. We also know that the siddhantas must have been written before Aryabhata. Hence one might give them a tentative date, say, the first half of the 5th century A.D.
According to Al-BirunI the Surya-Siddhanta was written by Lata, but it is probable that Lata was only responsible for its commentary. The text itself says that it was written by Surya, the Hindu Sun-God. Astronomical theories contained in it are of Greek origin, but much of the Hindu astronomical lores are also preserved. The most important feature of this work is the use of sines (jya) instead of chords. It also gives the earliest mention of a versed sine (utkramajya or utramadjya).
The Paulisa has been often quoted by Al-Biruni under the name Pulisa, which he said was the name of a Greek in Saintra (possibly Alexandria). This has suggested an identification of Paul of Alexandria, but it is impossible to substantiate this. The Paulisa is an important treaties on Hindu trigonometry. It gives the notion of the sine of an angle and contains a table of 24 sines in intervals of 3’45’, and also versed sines. The sine of 3’45′ is considered to be equal to the arc of 3’45’, i.e. sin 225′ = rad. 225′, or sin a = a where a = 225′. The arc of 225′ or a is called the kramajya. The other 23 sines up to 86T5′ were calculated using the rule:
![]()
In progress – stay tuned – equation in process of being copied
where n takes values 1, 2, 3 etc. for sin 2a, sin 3a, etc. The Paulisa gives a value of it = (sq rt)10, which is fascinating because of the fact that the same value was given in China by Chang Heng about the year 130 A.D.

About the year 499 A.D. Aryabhata wrote an important mathematical treatise, called the Aryabhattya, containing in a more systematic form the trigonometry in the Paulisa and many new results. He also developed the astronomy of the Siddhantas and added the theory of the rotation of the earth about its own axis. Aryabhata, the celebrated Hindu mathematician and astronomer, was born near Patna. During the year 3600 of Kaliyugi (about 499 A.D.) he wrote the Aryabhattya when he was only 23 years old. The book is divided into 4 parts. Parts 2 and 4 are often considered as a whole, called the Aryashtasata. The mathematics contained in the Aryabhattya include numeration by tens as far as 108, plane and solid numbers, a rule for finding square root, general solution c: indeterminate linear equations, solution of quadratic equations, sum of arithmetic series in the form:
![]()
Number of terms is an arithmetic series when the 1st term (a), the difference (d) and : – sum (s) are given, in the form:
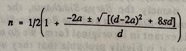
and an accurate value of
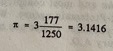
Aryabhata made a very daring hypothesis regarding the daily rotation of the earth. This was not accepted by later Hindu astronomers, such as Varahamihira and Brahmagupta.
At about the same time of Aryabhata, flourished the great Hindu astromer, mathematician and poet Varahamihira. There were two Indian astronomers with most celebrated writer on astronomy in early India. He wrote the Pancasiddhantika, a treatise on astronomy and astrology. It contains a summary of the five siddhantras in Karana form, that is, dealing with the practical side. He also quoted Aryabhata. The Pancasiddhantika had in fact superseded all previous Hindu works on astronomy and astrology. The treatise is divided into 3 parts, (a) on mathematical astronomy, (b) on the making of horoscopes and (c) on natural astrology and prognostications. He also wrote another treatise called the Brihatsamhita, a work on astrology, but also containing some information on precious stones, the geography of India and other topics, always from the astrological point of view. The Pancasiddhantika contains some trigonometrical rules equivalent to our modern formulae
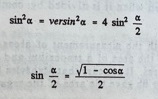
It appears that most of Varahamihira’s astronomy was derived from Greek sources. He said that the earth was spherical. Two of his works were translated into the Arabic by Al-Biruni.
The 7th century A.D. saw one of the greatest Hindu mathematicians. He was none other than Brahmagupta. In about the years 628 A.D. he wrote the Brahmasphuta-siddhanta, which is based upon the Surya-siddhanta and Aryabhata’s works, but also contains something original. Brahmagupta’s arithmetic includes work with integers and fractions, progressions, simple interest, mensuration of plane figures and simple solids. He gives the area of a quadrilateral as:
![]()
where a, b, c, d are the sides and s = 1/2(a + b + c + d). We know, however, that this is only true for a cyclic quadrilateral. He gives 2 different values for it, it = 3 as the “practical value” and it = (sq rt)10 the “neat value”. Brahmagupta applied algebra to astronomical problems. He gave a rule for solving a quadratic equation of the form x2 + px – q = 0, saying that
![]()
which we know gives only one of the 2 roots. He also dealt with simultaneous equations of the first degree and indeterminate equations. For the volume of the frustum of a pyramid with square bases of sides a and b he gave:
![]()
In about the 9th century A.D. lived the third of the great Hindu mathematical writers, Mahavira the Learned, who came from Mysore in south India. He wrote a treatise trying to improve upon the work of Brahmagupta. His treatment is generally treatise trying to improve upon the work of Brahmagupta. His treatment is generally fuller but of a more elementary nature than Brahmagupta’s. He was the only Hindu mathematician to deal with ellipes, though inaccurately. He dealt with arithmetic and geometric progressions and the summation of a series after a certain number of initial terms have been cut off. He stated an interesting rule in his treatment of fractions relating to the inverted divisor, saying:
“After making the denominator of the divisor its numerator (and vice versa), the operation to be conducted then is as in the multiplication (of fractions(* He also gave an interesting law relating to zero, i.e. “A number multiplied by zero is zero, and that (number) remains unchanged when it is divided by, combined with, (or) diminished by zero”.
Mahavira also dealt with the measurement of areas. However, he made the same mistake as Brahmagupta in the area of a trapezium and that of a quadrilateral by not limiting them to cyclic figures. It appears that Mahavira had known about the works of Chinese mathematicians, for he gave the area of the segment of a circle as:
![]()
There appeared also at about this time the Bakhshali manuscript, of uncertain date and origin. The work deals with arithmetic and algebra.
In the 10th century A.D. flourished the Hindu mathematician Srldhara or Srldharacarya. In about 1020 A.D. he wrote the Ganitasara (“Compendium of Calculation”), also given the subtitle Trisatika. It deals with series, squares, cubes, roots, interest, partnership, mensuration and shadow measurement. It makes an interesting statement about the zero:
If zero is added to a number, the sum is that number itself; if zero is subtracted, the number remains unchanged; if zero is multiplied, the result is zero; and if a number is multiplied by zero, the product is zero only”.
Note that he avoided the question of dividing a number of zero. In dividing a number by a fraction he gave the same rule as Mahavira, i.e. to multiply by the inverted divisor. Also like Mahavira he used it ![]() = (sq rt)10.
= (sq rt)10.
From the 10th to the 15th centuries there was only one other prominent writer in the history of Hindu mathematics. He was Bhaskara (114/c. 1185), also called Bhaskaracarya, i.e. Bhaskara the Learned. A temple inscription refers to him thus: “Triumphant is the illustrious Bhaskaracarya whose feet are revered by the wise, eminently learned,.. a poet, . . . endowed with good fame and religious merit. . . .”
Bhaskara wrote mainly on astronomy, arithmetic, mensuration and algebra. He is best-known for his treatise called Lilavati on arithmetic and mensuration. Lilavati was the name of his daughter; according to the predictions made by the astrologers, she would not be able to get married. But Bhaskara prognosticated a lucky moment for her marriage and left an hour cup floating on the vessel of water. The cup had a small hole in the bottom and was so arranged that the water would trickle in and sink it at the end of one hour. Lilavati was watching the water rising in the cup and did not notice that a jewel from her necklace had fallen and
was thus fated never to get married. To console her, Bhaskara wrote a book named after her and said, “I will write a book of your name which shall remain to the latest time; for a good name is a second life and the ground work of eternal existence.” The Lilavati includes notation, the operations with integers and fractions, the Rule of Three, interest, series, permutation, allegation, mensuration and a little algebra. It also gives the rules relating to the zero, although it wrongly says that o/o = o. Bhaskara also wrote a book on algebra, called the Bija Ganita, which deals with negative numbers, surds, etc., but not imaginary numbers, which Bhaskara brushed aside saying: “There is no square root of a negative quantity, for it is not a square”. A third book on astronomy called the Siddhanta Siromani (Head Jewel of accuracy) was also written by Bhaskara, who asserts that the earth is spherical.
During the. 11th century a commentary on the Susruta-samhita was written by the Bengali physician Cakrapanidatta, and in the following century another commentary was written by the Hindu physician Dallana. These are the two earlier commentaries extant of the Susruta-samhita. In the 13th century the Hindu physician Sarngadhara wrote a medical treatise wherein great importance was paid to mercurial and other metallic preparations. It also contained an elaborate analysis of the pulse. The great popularity of this work can be proved by the existence of many manuscripts and of many editions and translations into other Indian languages. The main feature of the work lies in its emphasis on the chemical side of materia medica. In the same century the Kashmirian physician Narahari composed a dictionary of materia medica called the Rajanighantu. In the second half of the 13th century Vopadeva wrote a commentary on the Sarngadharasamhita and other medical works. A medical treatise dealing with anatomy, physiology, general pathology and therapeutics was written by the Hindu physician Tlsatacarya. The treatise was entitled Cikitsakalika. A commentary to this work was later written by Tisatacarya’s son, Candrata.
We shall try to summarise the main features in Indian mathematics. Their best- known contributions to modern mathematics are their mathematical notations and their decimal system. In the Bakashali manuscript a small ‘plus’ sign, placed to the right of the quantity it refers to, is used to represent a negative quantity, while a dot represents zero. No symbols of operation are found in this manuscript.
It is of interest to note the method used in Hindu algebra for denoting the unknown quantity x. This they usually represented using the word ya (from yavat tavat, meaning ‘as many as’). For the second unknown y, they used the word ka (from kalaka, meaning ‘black’). For the constant they used the word ra (from the word rilpa). For the second power they indicated this by the letter v or the word va (from varga). Thus in the quadratic equations given by Sridhara, we have:
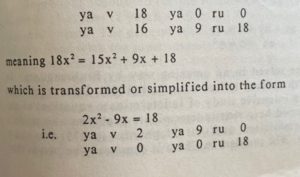
It is generally believed that the so-called Arabic numbers that we now employ were derived from India and that the Hindus had invented the place value of the decimal system and the nine digits and zero. There are certain quarters raising objection to this view, and some even said that the Hindus learned these from the Greek Neo-Platonists through Arabia. However, unless the contrary is proved in future through careful comparison of manuscripts for example, we ought not to deprive India of her claim to the honour of having originated the nine numerals and the zero.
The Hindus contribution to trigonometry deserves special attention. The Greek worked at first in terms of chords and expressed an angle by the ratio of the chord of a circle to its diameter. Ptolemy used a diameter = 120 for his chord. The Hindus took half the chord and a radius of 120.
Thus the sine of an angle is obtained. The Sanskrit word jya or jiva (meaning half-chord) became in the Arabic jiba and then jaib. When it was rendered to Latin it became sinus. Hence the modern word ‘sine’. As we know the sine first appeared in the words of Aryabhata, who also gave a table of sines. The sine also appeared in Varahamihira’s Panca a Siddhantika, where a table is constructed with the Greek diameter of 120. Bhaskara in the mid-12th century gave a method of constructing a table of sines for every degree.
The next trigonometrical function of interest to the astronomer was not the cosine, nor the tangent, but the versed sine (versin y = 1 – cos y). Known as utkramajya, the versed sine was mentioned as early as in the Surya-Siddhanta.
The cosine appeared in Aryabhata’s work as koti jya. The term did not come so quickly into general use, because the sine of the complementary angle would serve the same purpose.
The ancient astronomers in Egypt, in India and in China, for example, made use of the gnomon for measuring the sun’s shadow. Thus they were familiar with the measurement of the height of the gnomon and the length of the shadow, i.e., the height and the base of a right-angled triangle. However the tangent and the cotangent were only first used in the 9th century A.D. by the Arabs when Habash al-Hasib constructed the first tables of tangents and cotangents in c. 860 A.D. Some thought that the Indian shadow measurements had led to the use of these two trigonometrical functions by the Arabs.
Another point deserving special mention is the solution of indeterminate equations by the Hindus. These were of generally two types. Indeterminate equations of the first degree of the form:

These indeterminate equations were solved in an amazing way by Brahmagupta. In Europe we had to wait until the 17th century before John Pell (1668), Fermat (c. 1640) and Lord Brouncker (1657) made an intensive study of indeterminate equations of the quadratic type. It might be mentioned here that indeterminate problems also made a special appeal to the Chinese mathematicians, and that Diophantus (c. 275) also had a number of indeterminate equations. The problem in China is commonly known as that of the Hundred Fowls. This appeared to have found its way into Mahavira’s work in its problem of pigeons, birds and peacocks.
The conquest of Alexander the Great must have brought Greek Culture and knowledge to India. Although in mathematics there appeared to be many original contributions coming from India, it is generally believed that Indian astronomy is the offspring of Alexandrian science.
Before the coming of the Greeks, astronomy was not much developed in India. Some ideas had been acquired for the periods of the sun and the moon and the planet Jupiter (Vrihaspatis), which were used for chronological purposes. The movement of the moon was of special significance because it was connected with the proper time for making sacrifices. Other than these early Hindu astronomy appeared to be mainly astrology. There is no sign of any accurate knowledge of the planetary motion earlier than say the 3rd century A.D. The Hindu earth was a curved surface resting on 4 huge elephants. These four elephants in turn were supported on the back of a giant tortoise. The astronomical knowledge contained in the siddhantas showed a very strong Greek influence. For the first time the weeks of 7 days appeared in India. The names of the planets came from the Greek and the zodiacal signs have superceded earlier but also different star-groups (12 of them) connected with the motion of the sun. Many Greek geometrical, astronomical as well as astrological terms have gone into Sanskrit works. The influence of Greek astronomy was acknowledged by Hindu writers like Varaha- mihira.
In the siddhantas the earth is stated to be a sphere, and the ancient mythological concept that it was supported by elephants, and so on was rejected. Bhaskara Acharya, about 1150 A.D., also rejected the idea that the earth was continuously falling downwards, saying that if this was so an arrow shot upwards would never return to the earth’s surface. He said that all planets were moving round the earth with the same linear velocity. From this the relative distances of the planets from the earth were deduced, since their different periods could be observed. The diameter of the earth was considered to be 1600 yojans and the distance of the moon from the earth 51,570 yojans, i.e. 64.5 R, where R is the radius of the earth. Compare this with Ptolemy’s value of 64 1/6R. The planets moved in epicycles and the Hindus further added one of their own inventions, by assuming that the epicycle had a variable circumference, greatest when the planet is at apogee or perigee and least at 90° from these, giving rise to an oval epicycle. Some Hindu astronomers applied this oval epicycle to all planets, while others like Brahmagupta and Bhaskara applied this only to Mars and Venus, but there were also some who rejected this altogether.
Aryabhata accounted for the rotation of the earth by a strong air current extending to about 15 yojans (1 yojan = 7.6 miles) from the earth, whose diameter he considered to the 1050 yojans. The general opinion of the Hindus was that the planets were carried by mighty wind with the same velocity moving parallel to the ecliptic, but at the same time the planets were deflected from these courses by some invisible power. At the apogee this invisible force attracted the planet towards it cither from the left or from the right, at the node it diverted the planet from the ecliptic, first to one side and then to another, and finally at conjunction the force caused the planet to move with varying speed and to become occasionally stationary and even to move backwards, i.e., to retrograde. It is interesting to note the Hindu explanation of an eclipse. Brahmagupta, for example, advocated the existence of an eighth planet Rahu, which was the immediate cause of eclipse. However, such view was not shared by every Hindu astronomer, for example, Aryabhata.
Thus we see that Hindu astronomy consisted of a mixture of traditional mythology and a science based on observations and calculations. The latter is generally accepted as being of Greek origin. During the Middle Ages there was isolation between Europe and India. It was here that Hindu astronomy played an important though indirect role in influencing Western astronomy. The Arabs came into contact with the Indians and acquired from them astronomical knowledge which was later retransmitted back into Europe. We have already seen how the Arabs played their parts in this respect.
In the early 18th century the Hindu Maharaja Jai Sing II of Jaipur (1686/1743), after studying the methods of the European, the Muslim and the Hindu, constructed observatories in several parts of India, namely Jaipur, Delhi, Ujjain, Benares and Mathura. Jagannath, his chief astronomer, translated Euclid’s Elements and Ptolemy’s Almagest into Sanskrit. He employed Muslim astronomers to interpret Arabic star catalogues and the instruments used by Ulugh Beg at Samarkand. He sent his scholars to Europe and invited European scientists to Jaipur. Jai Singh was most influenced by the Muslim tradition of astronomy as exemplified in Ulugh Beg. He was essentially a practical man, paying attention to astrolabes and other astronomical instruments. His astronomical tables — the Zij Muhammad Shaji — appeared in 1728. Many of the instruments used by him still remain today. Among the instruments he used were the sundial (Nadi Yantra), the sphere (Gola Yantra), the azimuth instrument (Digamsa Yantra), the mural quadrant (Dakshino Digbhitt), the equinoctial dial (Samrat Yantra), the hemispherical dial (Jaya Prakas), and the 60° arc or sextant (Vritta Shashtamsaka).
